<< SEITE ZURÜCK Inhalt Kap. 1 Kap. 2 Kap. 3 Kap. 4 Kap. 5 SEITE WEITER >>
Vorlesung Strukturchemie der Oxide
3. Binäre Metalloxide

3.3. Normale Metalloxide

Bevor die wichtigsten Strukturtypen der Metalloxide im Detail vorgestellt werden, soll zunächt ein allgemeiner Überblick über physikalische Eigenschaften, die chemische Bindung und die wichtigsten strukturbestimmenden Faktoren gegeben werden. Die meisten Metalloxide etwa bis zur Oxidationsstufe +4 bilden echte Ionenkristalle (und damit demnach dreidimensional zu beschreibende Verbände). Bei den Übergangsmetalloxiden höherer Oxidationsstufen finden sich dann eher kovalent aufgebaute Verbindungen mit niederdimensionalen Verbänden. Beispiele hierfür sind molekulare Verbindungen wie Mn2O7 oder RuO4, Kettenstrukturen wie CrO3 und Schichten in V2O5, MoO3 oder Re2O7. Nicht nur strukturell sondern auch aufgrund der physikalischen Eigenschaften sind die Metalloxide damit bei weitem keine einheitliche Klasse. Beispielweise variieren die Schmelzpunkte von sehr hochschmelzenden Verbindungen wie z.B. HfO2 (Mp 2800 oC) und den molekularen Phasen wie z.B. Mn2O7 (Mp. 6oC) stark. Auch die elektrischen Eigenschaften reichen von Isolatoren (MgO) bis zu guter metallischer Leitfähigkeit (ReO3). Viele Übergangsmetalloxide zeigen darüberhinaus interessante physikalische Eigenschaften: Z.B. sind EuO und CrO2 ferromagnetisch, viele Übergangsmetall-Oxide MO zeigen anormales elektrisches und magnetisches Verhalten (z.B. NiO). Aufgrund dieser Eigenschaften finden viele Oxide ausgedehnte technische Verwendung (z.B. CrO2 für Magnetbänder). Aber auch als Grundstoffe in der Großindustrie sind Metalloxide von sehr großer Bedeutung. Beispiele hierfür sind die Verwendung als Pigmente (z.B. TiO2), Füllstoffe oder Absorber-Materialien (z.B. Al2O3).
Strukturell lassen sich alle Metalloxide, die nicht durch gerichtete Bindungen bestimmt werden (das ist der Hauptteil!) wie viele andere Ionenkristalle durch die Füllung von oktaedrischen und tetraedrischen Lücken in dichtesten Packungen beschreiben, da der Ionenradius von O2- mit 140 pm deutlich grösser ist als die Radien der meisten Metallkationen. Abweichungen von diesem Konzept treten bei den Übergangsmetallen auf, wo zusätzlich zu rein geometrischen Verhältnissen Kristallfelder eine Rolle spielen.
Besonders bei den Übergangsmetalloxiden finden sich neben den Daltoniden (stöchiometrische Verbindungen) oft nichtstöchiometrische Phasen (z.B. W-Oxide, Fe-Oxide.).
Die untenstehende Tabelle gibt eine Übersicht über alle stöchiometrischen Metalloxide. Geordnet nach Oxidationsstufe sind die jeweils auftretenden Strukturtypen angegeben. Auf die Angabe von gemischtvalenten Phasen und Phasenbreiten muß hierbei verzichtet werden.
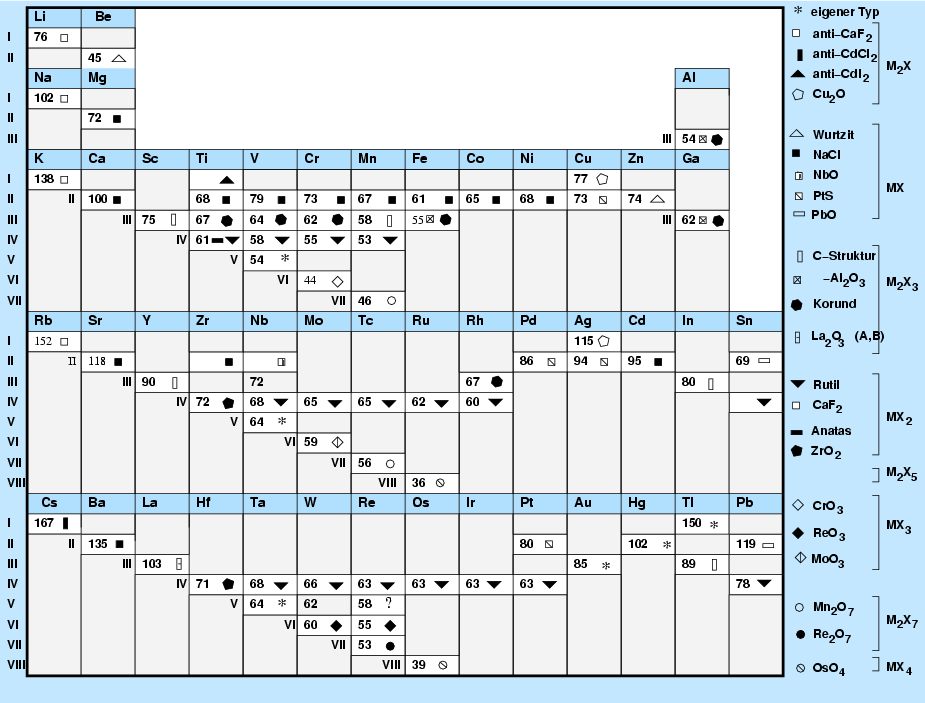
Abb. 3.3.1. Struktur der Metall-Oxide im Periodensystem
Die Symbole in Abb. 3.3.1. bedeuten im Einzelnen Vor der Besprechung der Oxiden im Einzelnen sollen zunächst die strukturbestimmenden Faktoren und die chemische Bindung in Ionenkristallen kurz wiederholt werden ( 3.3.1) Die systematische Strukturklassifizierung auf der Basis dichter Packungen folgt unter 3.3.2. Im Abschnitt 3.3.3 werden die wichtigsten Oxide nach Stöchiometrie im Detail besprochen.

3.3.1 Ionenkristalle: Chemische Bindung und Konzepte der Strukturchemie

Die überwiegende Zahl binärer Metalloxide (bis etwa zur Oxidationsstufe +4) sind mehr oder weniger ionisch aufgebaute Verbindungen. Der Ionencharakter läßt sich z.B. nach Pauling (gemäß 1 - e-1/4(xA-xB)) ermitteln und liefert die folgenden Werte:
Verbindung LiF MgO FeO OsO4
Ionencharakter nach Pauling 0.9 0.73 0.52 0.35

Qualitative Betrachtung: Ionische Verbindungen werden durch elektrostatische Kräfte zusammengehalten; die Anionen sind von Kationen umgeben und umgekehrt. Eine große elektrostatische Anziehung, d.h. eine große Gitterenergie wird dabei durch hohe Koordinationszahlen erreicht. Kontakte der Anionen bzw. Kationen untereinander sollten minimal, Kontakte zwischen Anionen und Kationen maximal sein. Gleichzeitg muß lokale elektrostatische Neutralität erreicht sein.

Quantitative Betrachtung Bei kleinen Drücken verbleibt von der Gibbs-schen freien Energie (G = E - TS + PV) nur die Helmholtz-Energie als wesentlicher Beitrag: F = E - TS. Die innere Energie E des Kristalls besteht dabei aus zwei Anteilen (E = UL + EV), dem dynamischen Anteil EV und der statischen Gitterenergie UL. Diese Gitterenergie ist wiederum die Summe verschiedener Anteile: (in Klammern typische Prozentangaben zum Beitrag an der gesamten Gitterenergie:
UL = Ea (80%) + Er (10-15%) + Es (5-10%) + kovalente Bindungsanteile + van der Waals + ..
Die Anteile sind (Z=Ladungen, R=Gleichgewichtsabstand, B=Proportionalitätskonstante)

Ea und Er zusammen hängen (unter Vernachlässigung der Ligandenfeldstabilisierungsenergie) nur vom Abstand der Ionen, deren Ladungen sowie dem Strukturtyp ab:
Ea + Er = UL = - [ { A N0 z1 z2 e2} / {Re} ] (1- 1/n)
Typische Werte für die Madelungkonstante A sind:
Strukturtyp NaCl Rutil Anatas Fluorit
Madelungkonstante A 1.76 2.408 2.400 2.519

UL kann experimentell z.B. auf der Basis des Born-Haber-Kreisprozeßes bestimmt werden. Danach ist die treibende Kraft für die Bildung eines Ionenkristalls (d.h. die Bildungsenthalpie) zusammengesetzt aus:

ΔHf = ΔHM + ΔHx + ΔHIE + ΔHEA + UL
wobei:
Einige Werte für die Gitterenergien:
Verbindung NaCl MgO BaO
Gitterenergie UL -760 kJ/mol -4000 kJ/mol -3200 kJ/mol
Schmelzpunkt [oC] 800 2800 1900

Man sieht, daß die Schmelzpunkte etwa parallel mit der Gitterenergie variieren.
Die qualitative Folgerung für die maximale Gitterenergie ist, daß die Kationen von möglichst vielen Anionen umgeben sein sollten (und umgekehrt) und Kationen und Anionen �zueinander passen� sollen.

In der Strukturchemie von Ionenkristallen gibt es hierzu einige empirische Regeln (sog. Pauling-Regeln):

1. Pauling'sche Regel Für die Polyeder um die Kationen gilt, daß der Abstand Kation-Anion durch die Summe, die Koordinationszahlen durch das Verhältnis der Ionenradien bestimmt wird (sog. Radienverhältnisregel). Demnach bestimmt also das Radienverhältnis wesentlich die Koordinationszahl und damit auch den möglichen Strukturtyp. Konkret folgt für die Koordinationszahlen der Kationen in Oxiden (rein geometrische Betrachtung, Ligandenfelder vernachlässigt, Radius von O2- = 140 pm):
CN=4 (Tetraeder) CN=6 (Oktaeder) CN=8 (Würfel)
Radienverhältnis (untere Grenze) 0.225 0.414 0.732
Kationenradius in Oxiden [pm] 36 58 102
Zusammensetzung Strukturtypen
A2B anti-CaF2 - -
AB ZnS (Zinkblende, Wurtzit) NaCl CsCl
AB2 SiO2 Rutil, CdCl2, CdI2 CaF2
Die Strukturen lassen sich zum großen Teil wegen der Ionenradien als dichte Packungen aus O2--Ionen mit gefüllten Lücken beschreiben.

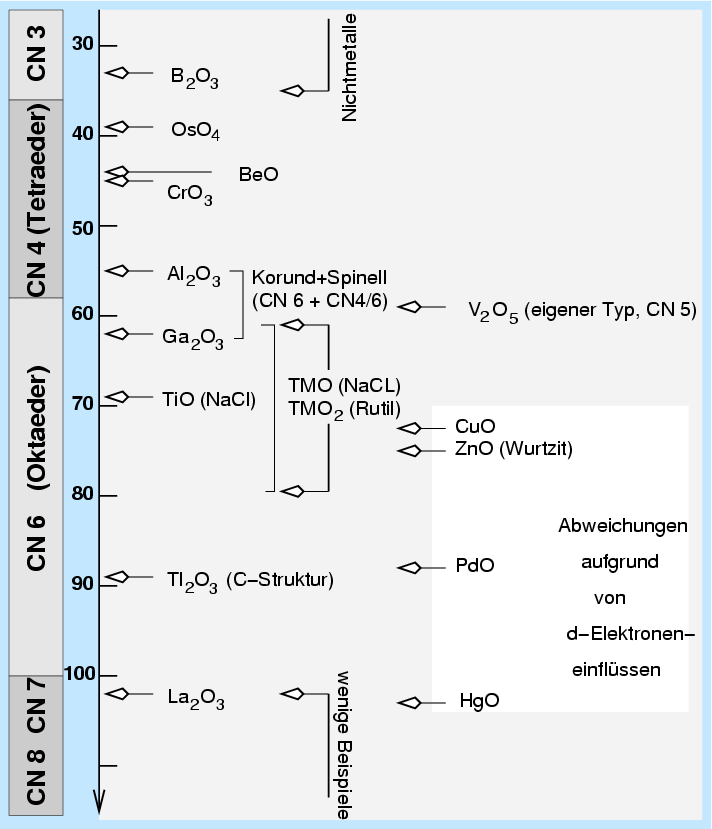
Abb. 3.3.2. Radienverh"altnisregel an Beispielen
Die Überprüfung der Radienverhältnisregel an Beispielen (s. Abb. 3.3.2.) zeigt, daß sie nur bedingt gilt. Abweichungen finden sich vor allem bei den späten Übergangsmetallen (Cu,Zn) und den Alkali- und Erdalkalimetallen. Ein Teil dieser Abweichungen wird verständlich, in den Fällen, in denen die innere Elektronendichte eines Ions nicht kugelsymmetrisch ist. Hier sind zwei Fällen denkbar:
  1. Inert-Pair Einfluß für Hauptgruppenmetalloxide mit (maximaler Oxidationszahl-2)
  2. Ligandenfeldeinfluß für nicht vollbesetzte d-Schalen (bei den Übergangsmetallen)
zu 1: Inert-Pair Einfluß

Bei Hauptgruppenmetalloxiden mit der (maximalen Oxidationsstufe-2) (z.B. Sn2+, Pb2+) kommt es zu einer Verzerrung der Metall-Sauerstoff-Koordination durch das einsame Elektronenpaar. Z.B. sind im Pb2+-Oxid die 6 s2-Elektronen stereochemisch aktiv (sp-Hybrid), so daß PbO und und auch SnO eine tetragonal verzerrte CsCl-Struktur ausbilden.

zu 2: Ligandenfeldeinfluß

In die Gitterenergie UL gehen bei Übergangsmetallionen mit unvollständig gefüllten d-Elektronenschalen neben den elektrostatischen Anteilen Ea und Er (anziehender und abstoßender Teil) und kovalente Bindungsanteile, van der Waals Anteilen usw. auch Ligandenfeldstabilisierungsenergien (LFSE, Es) ein. Die Gitterenergie ist damit in diesen Fällen entsprechend größer. Der Einfluß der d-Elektronen auf das Koordinationspolyeder um Übergangsmetall-Kationen ist aus der Komplexchemie bekannt: aus der Ligandenfeld-Theorie folgt, daß die Ligandenfeldstabilisierungsenergie (LFSE) bestimmt, welches Ion welche Koordination (hier gegen den Liganden O2-) bevorzugt. Während sich in den isolierten Kationen alle d-Orbitale auf dem gleichen energetischen Niveau befinden, wird bei der LF-Theorie der Einfluß der Liganden (die zunächst als Punktladungen betrachtet werden) auf die Energieniveaus der verschiedenen d-Orbitale betrachtet. Beispielsweise geben sich im oktaedrischen und im tetraedrischen Ligandenfeld Aufspaltungen der d-Orbitale in zwei Gruppen:

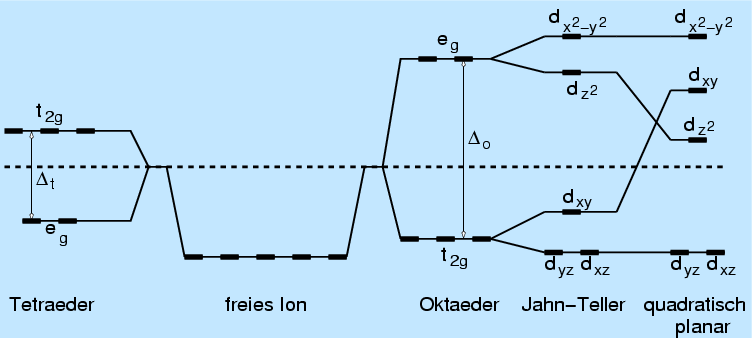
Abb. 3.3.3. Ligandenfeldabspaltung in nichtkugelsymmetrischen Kristallfeldern
  1. Die dxy-, dxz- und dyz-Orbitale weisen auf die Diagonalen des Koordinatensystems (t2g-Zustände).
  2. Das dx2-y2- und das dz2 liegen dagegen auf den Koordinatenachsen (eg-Zustände).
Im oktaedrischen Feld werden entsprechend der Abstoßung Ligand - d-Zustand die t2g Zustände entsprechend dem Schwerpunktsatz energetisch erniedrigt, während im tetraedrischen Ligandenfeld die Verhältnisse genau umgekehrt sind. Die Größe der Energieaufspaltung wird sowohl von der Art des Liganden als auch vom Metallatom bestimmt. Generell gilt, daß die Aufspaltung im oktaedrischen Ligandenfeld etwa doppelt so groß ist wie die im tetraedrischen Fall. Die Aufspaltung im oktaedrischen Feld (Δo) liegt allgemein im Bereich von 70 bis 350 kJ/mol, bei Oxiden bei 70-160 kJ/mol. Sie wird bestimmt durch: Die Kristallfeldstabilisierungsenergie (die in die Gitterenergie direkt mit eingeht) ist die Energie, die durch Einfüllen der Elektronen in die jeweils niedrigeren Niveaus gewonnen wird. Die Besetzung der Zustände folgt i. A. dem Pauli-Prinzip, die Spin-Paarungsenergie bestimmen, ob High-Spin oder Low-Spin-Systeme gebildet werden. Da die Aufspaltung im oktaedrischen Feld etwa doppelt so groß ist, wie die im tetraedrischen Feld, wird bei Kationen mit d3, d4, d6, d7 und d8-Elektronenkonfiguration i.A. die oktaedrische Umgebung bevorzugt (sog. Octahedral Site Preference Energy). Die folgende Tabelle gibt einen Überblick über das Ausmaß der Bevorzugung:
Elektronen- Oktaeder- Tetraeder-
konfiguration Ion Stabilisierung Stabilisierung Differenz
d3 Cr3+ 225 67 158
d5 Fe3+ 0 0 0
d6 Fe2+ 50 33 17
d8 Ni2+ 122 36 86
d10 Zn2+ 0 0 0
Dieser Einfluß der d-Elektronenverteilung macht sich bei den verschiedenen Oxiden unmittelbar bemerkbar:

Zusammenfassend (Kap. 3.3.1.) läßt sich feststellen, daß die Metalloxide i.a. als dichte Packungen von O2- mit Kationen in den Lücken beschrieben werden können. Die Koordinationszahl um das Kation wird vom Radienverhältnis Anion-Kation (1.Pauling'sche Regel) bestimmt. Die LFSE bewirkt (bei Übergangsmetallionen mit entsprechender d-Elektronenkonfiguration) zusätzlich eine Bevorzugung der oktaedrischen Umgebung. Weitere Details der Elektronenkonfiguration bestimmen das Ausmaß der Jahn-Teller-Verzerrung (CuO), die im Extremfall (PdO, PtO) bis zu quadratisch planarer Umgebung führen kann. Der Inner-Pair-Effekt kann für Hauptgruppenmetalloxide mit (maximaler Oxidationsstufe - 2) ebenfalls die Koordinationsgeometrie der O-Anionen um die M-Kationen bestimmen.

Die Gesamtstruktur folgt aus der Art der Verknüpfung der MOn-Polyeder. Die Verknüpfung sollte dabei in der Weise erfolgen, daß gleichnamige Kontakte maximiert und ungleichnamige minimiert werden. Für die Art der Polyederverknüpfung gilt die

3. Pauling-Regel : Gemeinsame Kanten und besonders gemeinsame Flächen destabilisieren eine Struktur. Dies gilt insbesondere für hochgeladene Kationen mit kleiner Koordinationszahl.

Bei den verschiedenen Modifikationen des TiO2 läßt sich die Auswirkung dieser Regel direkt erkennen: Die Rutil-Modifikation (Verknüpfung über zwei gemeinsame Kanten ist stabiler als Brookit (drei gemeinsame Kanten), dieser ist wiederum stabiler als Anatas (vier gemeinsame Kanten).

3.3.2. Struktursystematik auf der Basis dichter Packungen

Auf der Seite zu dichten Packungen findet sich eine Struktursystematik von Ionenkristallen auf der Basis gefüllter Lücken in dichtesten Packungen der Anionen, in die auch die meisten Oxide einbezogen werden können. (S. hierzu auch die Vorlagen mit den Schemazeichnungen).

Zusätzliche Anmerkungen:

3.3.3. Metalloxide nach Zusammensetzungen

Im folgenden werden für alle Metalloxide (geordnet nach Zusammensetzung) die Strukturen diskutiert, wobei auf die unter 3.3.1 (z.B. LFSE) und 3.3.2 (Packungen) genannten Punkte jeweils hingewiesen wird. Von der Diskussion ausgenommen sind die Suboxide und Oxide mit O-O-Bindungen sowie nichtstöchiometrische und z.T. auch gemischtvalente Oxide.

<< SEITE ZURÜCK Inhalt Kap. 1 Kap. 2 Kap. 3 Kap. 4 Kap. 5 SEITE WEITER >>